Relational Model

Data represented in a relational model as a table. In the table, there are attributes as columns and tuple data as rows.

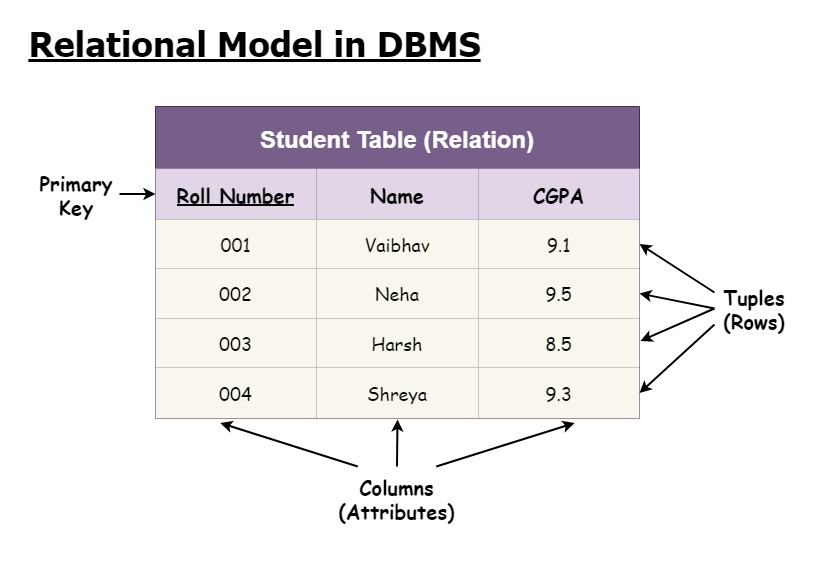
Further, we give out the mathematical definition for the relational model. The data in a database should be unordered and repeated, which means a dimension of data, called attributes. In the example above, the attributes can be described into sets, $A\text{for Name Attribute},B\text{for CGPA Attribute}$$A\ \text{for Name Attribute}, B\ \text{for CGPA Attribute}$. The table above can be described as a space spanned by the two dimension of sets using Cartesian Product

Now, we are confident to give the concrete definition and have a clear mind of what a relational model. The relational schema can be seen as a combination of attributes, written as $R(A_1,...,A_n)$$R(A_1, ..., A_n)$. Hope you still remember the notion of schema and instance. We often use $r(R)$$r(R)$ as a notation for an instance according to a relational schema $R$$R$.

The data space of an attribute, value without repetition, is the domain of the attribute. The special value null is a member of every domain. Indicated that the value is “unknown”. If you have some experience about machine learning task, like kaggle, you might be aware that the null data is the first thing you need to take care of.

Keys

Before we look into keys, we first need to make a clarification about the symbol $\in$$\in$, which means "belongs to" or "is an element of; and the symbol $\subset$$\subset$, which is a relationship between attributes combinations. The "belongs to" is used when a tuple belongs to a relational model $t\in r(R)$$t\in r(R)$. The subset is used to describe the attributes combination relationship, like $\{ID,Names\}\subset R$$\{ID, Names\}\subset R$

Then, there are some special attributes that can help us to better design the database schema.

• SuperKey: A attribute or a combination of attributes $K$$K$ can be defined as a superkey if $K$$K$ itself is enough to identify a unique tuple in a relation model.

  • Example: {ID, Name} and {ID} are superkeys for Students Relation

  • There can be more than one superkeys in one relational model

• CandidateKey: Among all the possible superkeys in $R$$R$, the superkey with the minimal number of attributes is the candidatekey.

  • There can be more than one candidatekeys for $R$$R$

• PrimaryKey: One of the candidate key is selected as primary key

• Foreign Key: There are always more than one relational entity in a database. Because those entities are connected with logical behaviors, this lead to the attributes called foreignkeys.

  • Example: dept_name in instructor is a foreign key from instructor referencing department

Relational Algebra

Relational algebra is a formal way for query language using mathematics. We will mainly focus on six operation in relational algebra.

Select $\sigma$$\sigma$

The select operation selects tuples that satisfy a given predicate.

In relational algebra, the select operation (σ) is used to select tuples (rows) from a relation (table) that satisfy a given predicate (condition). Here's an example using the instructor relation to select those tuples where the instructor is in the "Physics" department:

Given Relation: instructor

Query: ${\sigma }_{Deptname=Physics}(instructor)$$σ_{Deptname= Physics} (instructor)$

Resulting Relation:

The query σ Dept_name = "Physics" (instructor) selects all tuples from the "instructor" relation where the "Dept_name" attribute is equal to "Physics," resulting in the two tuples (John and Bob) that meet this criteria.

In relational algebra, you can use various comparison operators, like $=,\ne ,>,\ge ,<,\le$$=, \neq, >, \ge, <, \le$ and logical connectives $\wedge ,\vee ,\mathrm{\neg }$$\and, \or, \neg$ to create complex selection predicates. Here are some examples using the given operators and connectives:

1. Find the instructors in the "Physics" department with a salary greater than $90,000:

   Query: ${\sigma }_{deptname=Physics\wedge salary>90,000}(instructor)$$σ_{deptname=Physics ∧ salary > 90,000} (instructor)$

2. Find all departments whose name is the same as their building name:

   Query: ${\sigma }_{deptname=building}(department)$$σ_{deptname = building} (department)$

In the first example, we use the ∧ (and) operator to combine two conditions: one for the department name and another for the salary. Only rows that satisfy both conditions (in the "Physics" department and a salary greater than $90,000) will be selected.

In the second example, we compare the "dept_name" attribute with the "building" attribute within the "department" relation to find departments where the name matches the building name. This is a self-comparison within the same relation.

Projection $\mathrm{\Pi }$$\Pi$

In relational projection is denoted by the symbol $\mathrm{\Pi }$$\Pi$. It returns a new relation with a subset of attributes (columns) from the original relation, and it removes duplicate rows since relations are treated as sets.

The notation for the projection operation is as follows:

• π represents the projection operation.

• A1, A2, A3, ..., Ak are the attribute names you want to retain in the result.

• r is the name of the original relation (table).

Here's an example to illustrate how the projection operation works:

Given Relation: student

Query:${\mathrm{\Pi }}_{ID,Name}(student)$$\Pi_{ID, Name} (student)$

Resulting Relation:

In this example, the projection operation π ID, Name (student) selects only the "ID" and "Name" attributes from the "student" relation, resulting in a new relation with only those two attributes. Duplicate rows are removed in the result, as relations are considered sets, and sets do not contain duplicate elements.

Composition of Relational Operations

In relational algebra, you can compose multiple relational operations together to form more complex queries. This is achieved by using the result of one operation as the input to another operation within the same expression. The result of each operation is a relation, and these operations can be nested or combined to retrieve the desired information.

As you've mentioned, you can give an expression that evaluates to a relation as an argument to a relational operation. Let's break down your example query:

Query: Find the names of all instructors in the Physics department

You can compose this query using relational algebra operations as follows:

1. Selection (σ): First, you select the tuples (rows) in the "instructor" relation where the department is "Physics."

   Query: $$

2. Projection (π): Next, you project the "name" attribute from the result obtained in step 1 to get the names of instructors in the Physics department.

   Query: ${\mathrm{\Pi }}_{name}({\sigma }_{deptname=Physics}(instructor))$$\Pi_ {name }(σ_{deptname = Physics}(instructor))$

This expression first performs the selection operation to filter instructors in the "Physics" department and then projects the "name" attribute from the resulting relation.

The final result will be a relation consisting of only the "name" attribute, containing the names of all instructors in the Physics department.

Union $\cup$$\cup$

The union operation in relational algebra allows you to combine two relations, but there are specific conditions that must be met for the operation to be valid, as you've mentioned:

• Both relations, denoted as r and s, must have the same arity, meaning they must have the same number of attributes (columns).

• The attribute domains of corresponding attributes in r and s must be compatible. This means that the data types or domains of attributes that align with each other in both relations must be the same or compatible. For example, if the 2nd column of relation r deals with integer values, the 2nd column of relation s must also deal with integer values.

The union operation is denoted by the symbol $\cup$$\cup$, and it combines the rows from two relations while ensuring that duplicates are removed, as relations are treated as sets.

Here's an example of using the union operation to find all courses taught in either the Fall 2017 semester or the Spring 2018 semester, or both:

Given Relations:

1. "section" relation:

Query: $({\mathrm{\Pi }}_{courseID}({\sigma }_{semester=Fall\wedge year=2017}(section)))\cup ({\mathrm{\Pi }}_{courseID}({\sigma }_{semester=Spring\wedge year=2018}(section)))$$(\Pi _{courseID} (σ _{semester = Fall ∧ year = 2017} (section))) \cup(\Pi _{courseID}(σ _{semester = Spring ∧ year = 2018} (section)))$

Resulting Relation:

In this example, we first use the selection operation (σ) to filter courses taught in the Fall 2017 semester and separately courses taught in the Spring 2018 semester. Then, we use the projection operation (π) to select only the "course_id" attribute from each of these filtered relations. Finally, we apply the union operation (⋈) to combine the results into a single relation, ensuring that duplicate rows are removed, resulting in a list of courses taught in either semester or both.

Set-Intersection $\cap$$\cap$

The set-intersection operation in relational algebra, denoted as ⋂, allows you to find the tuples that exist in both input relations. Here are the conditions for this operation:

1. Both relations, denoted as r and s, must have the same arity, meaning they must have the same number of attributes (columns).

2. The attributes of r and s must be compatible, which means the data types or domains of corresponding attributes in both relations must be the same or compatible.

Here's an example of using the set-intersection operation to find the set of all courses taught in both the Fall 2017 and the Spring 2018 semesters:

Given Relations:

1. "section" relation:

Query:

Resulting Relation:

In this example, we first use the selection operation (σ) to filter courses taught in the Fall 2017 semester and separately courses taught in the Spring 2018 semester. Then, we use the projection operation (π) to select only the "course_id" attribute from each of these filtered relations. Finally, we apply the set-intersection operation (⋂) to find the common course IDs that exist in both filtered relations.

In this case, there are no common courses taught in both the Fall 2017 and Spring 2018 semesters, so the result is an empty relation (no rows).

Set Difference -

The set-difference operation in relational algebra, denoted as "-", allows you to find tuples that are in one relation (r) but not in another relation (s). Here are the conditions for this operation:

1. Both relations, denoted as r and s, must have the same arity, meaning they must have the same number of attributes (columns).

2. The attribute domains of r and s must be compatible, which means the data types or domains of corresponding attributes in both relations must be the same or compatible.

Here's an example of using the set-difference operation to find all courses taught in the Fall 2017 semester but not in the Spring 2018 semester:

Given Relations:

1. "section" relation:

Query:

Resulting Relation:

In this example, we first use the selection operation (σ) to filter courses taught in the Fall 2017 semester and separately courses taught in the Spring 2018 semester. Then, we use the projection operation (π) to select only the "course_id" attribute from each of these filtered relations. Finally, we apply the set-difference operation ("-") to find the course IDs that exist in the Fall 2017 semester but not in the Spring 2018 semester. The result includes courses taught in the Fall 2017 semester but not in the Spring 2018 semester.

Cartesian Product $\times$$\times$

The Cartesian product operation (denoted by ⨯) in relational algebra allows you to combine information from two relations by forming all possible pairs of tuples, one from each relation. This operation results in a new relation with a combination of attributes from both input relations. It is sometimes referred to as the cross product.

Here's an example using the "instructor" and "teaches" relations:

Given Relations:

1. "instructor" relation:

2. "teaches" relation:

The Cartesian product of these two relations, written as "instructor ⨯ teaches," combines every tuple from the "instructor" relation with every tuple from the "teaches" relation, forming all possible pairs:

Resulting Relation:

As you can see, the result includes all possible pairs of tuples from both relations, and attributes from each relation are prefixed with the relation name to distinguish them, such as "instructor.ID" and "teaches.ID." The resulting relation has a combined schema containing attributes from both input relations.

However, when you perform the Cartesian product (⨯) between two relations, it creates a combination of every tuple from the first relation with every tuple from the second relation. This can result in a large number of combinations, many of which may not be meaningful in a given context.

To filter the result to only include combinations that are meaningful, you can use the selection operation (σ) with a condition that matches the related attributes in both relations. This effectively restricts the result to tuples that represent valid associations between the two relations.

To get only those tuples of "instructor ⨯ teaches" that pertain to instructors and the courses they taught, you can use the selection operation with the condition "instructor.ID = teaches.ID":

Query: ${\sigma }_{instructor.ID=teaches.ID}(instructor⨯teaches)$$σ _{instructor.ID = teaches.ID} (instructor ⨯ teaches)$

Resulting Relation:

In this result, you only get tuples that represent instructors and the courses they taught, filtering out combinations that do not correspond to actual teaching assignments.

Join $\bowtie$$⋈$

The join operation in relational algebra combines the selection operation and the Cartesian product operation into a single operation. It allows you to create meaningful associations between two relations based on a specified predicate.

The join operation, denoted as r ⋈𝜃 s, is defined as follows:

Here, r and s are two relations, and 𝜃 is a predicate on attributes that can be applied to both r and s. The result of the join operation is obtained by first taking the Cartesian product (r × s) and then applying the selection (σ) operation with the predicate 𝜃.

Using your example of joining the "instructor" and "teaches" relations based on the predicate "instructor.ID = teaches.ID," you can write it as follows:

This expression performs the join between the "instructor" and "teaches" relations, filtering the result to only include tuples where the "ID" attribute in the "instructor" relation matches the "ID" attribute in the "teaches" relation. This gives you a meaningful association between instructors and the courses they taught, just like using the selection operation on the Cartesian product, as you mentioned earlier.

Assign

The assignment operation in relational algebra, denoted by ← (like assignment in a programming language), allows you to assign the result of an operation to a temporary relation variable. This is particularly useful when you want to break down a complex query into a sequence of steps for clarity and reusability.

Here's an example using the assignment operation to find all instructors in the "Physics" and "Music" departments:

xxxxxxxxxx
Physics ← σ dept_name = "Physics" (instructor)
Music ← σ dept_name = "Music" (instructor)
Result ← Physics ⋃ Music

In this example:

1. Physics ← σ dept_name = "Physics" (instructor) assigns the result of selecting all instructors in the "Physics" department to a temporary relation variable called "Physics."

2. Music ← σ dept_name = "Music" (instructor) assigns the result of selecting all instructors in the "Music" department to a temporary relation variable called "Music."

3. Result ← Physics ⋃ Music combines the two previously assigned relations "Physics" and "Music" using the union operation (⋃) and assigns the result to a temporary relation variable called "Result."

By breaking down the query into these steps, you can see the intermediate results and make the query more readable and understandable. The final result is stored in the "Result" relation variable, which can be used further or displayed as the output of the query.

Rename

The rename operation in relational algebra, denoted by $\rho$$\rho$ allows you to assign a specific name to the result of a relational-algebra expression. This is particularly useful when you want to give a meaningful name to the result so that you can reference it in subsequent operations or queries.

The notation for the rename operation is as follows:

• ρ represents the rename operation.

• X is the name you want to assign to the result of expression E.

• E is the relational-algebra expression whose result you want to name as X.

For example, suppose you have a query to find all instructors in the "Physics" department:

xxxxxxxxxx
PhysicsInstructors ← σ dept_name = "Physics" (instructor)

In this case, you've created a temporary relation called PhysicsInstructors to hold the result. Now, if you want to use this result in subsequent operations, you can use the rename operation to give it a more meaningful name:

xxxxxxxxxx
PhysicsInstructorsRenamed ← ρ PhysicsInstructors (PhysicsInstructors)

Now, PhysicsInstructorsRenamedis the renamed relation containing the same data as PhysicsInstructors but it has a more descriptive name that you can reference in future expressions or queries.